Lion Wall: Building a character-matching game
Table of Contents
| App | https://jbuckland.com/games/lionwall |
|---|
Background⌗
Lion Wall is an online game inspired by Only Connect, a British TV quiz show. In the third round of Only Connect, contestants are faced with a four-by-four grid of cards. These cards can be grouped into four sets of four, where group is connected by some common thread.

An example “Connecting Wall” puzzle. The answer requires dividing the items into “Terms for zero”, “Poker terms”, “Flying ___” and “Things made of rubber”.
Red Herrings⌗
To make the puzzle harder, some of the cards seem to belong to more than one category. In the example above, the category “Poker terms” applies to “Deuce”, “Bullet”, “Crab”, and “Cowboy”.
This category also seems as though it ought to apply to “Ace”, but “Ace” actually belongs to the category “Flying ___”.
On Only Connect, these cards are called red herrings.
Generalizing the Connecting Wall⌗
I first wanted to lift this game out of the domain of English-language trivia.
- Let each of [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] represent a category in the abstract.
- The values [1, 2, 3, 4] will be special “real” categories. The others will be “red herring” categories.
- Let a card consist of an unordered list of categories.
- Each card must contain exactly one of [1, 2, 3, 4].
I constructed a generalized Connecting Wall game:
[ [ (1, 5), (1, 6), (1, 7), (1, 8) ]
, [ (2, 6), (2, 7), (2, 8), (2, 9) ]
, [ (3, 0), (3, 7), (3, 8), (3, 9) ]
, [ (4, 0), (4, 5), (4, 6), (4, 9) ]
]
such that the special “real” categories [1, 2, 3, 4] are mentioned in exactly four cards each, with no overlaps, and the “red herring” categories [0, 5, 6, 7, 8, 9] are mentioned in three or fewer cards each.
If we wanted to map this generalized game back to an English-language trivia game, the real categories [1, 2, 3, 4] might become ["Terms for zero", “Poker terms”, “Flying ___”, “Things made of rubber”], and the red herring categories might become more loosely-defined categories such as:
- “Starts with B” (Buttress, Bullet),
- “Animal” (Crab, Fox, Fish, Goose-egg?), or
- “Contains a repeating letter” (Goose-egg, Buttress, Bullet), etc.
Specifying for CJK characters⌗
Many CJK characters consist of two subcomponents: if we map each of the categories 0-9 to a component, we can usually find characters which contain only those two components.
By hand⌗
Before writing an automated solution, I stepped through the process of assembling a valid puzzle by hand. I picked ten common radicals and mapped them to the numbers 0-9:
0 九
1 疒
2 宀
3 犭
4 口
5 了
6 丁
7 主
8 由
9 示
Then, for each card in the generalized grid above, I tried to find a character which matched:
15 疒了 疗
26 宀丁 宁
30 犭九 犰
40 口九 㕤
16 疒丁 疔
27 宀主 宔
37 犭主 㹥
45 口了 𠮩
17 疒主 疰
28 宀由 宙
38 犭由 㹨
46 口丁 叮
18 疒由 㾄
29 宀示 宗
39 犭示 狋
49 口示 呩
This got me a valid puzzle:
疗 宁 犰 㕤
疔 宔 㹥 𠮩
疰 宙 㹨 叮
㾄 宗 狋 呩
This puzzle is unshuffled as drawn above. You can see that each character in the first row contains 疒; each character in the second row contains 宀; then 犭, then 口.
Automating⌗
Similar to AutoCJK, I used the phenomenal resource IDS.TXT as a backing dataset. I reused the decomposition utilities from AutoCJK which know how to read/parse IDS.TXT. In short, running decomposer.Decomposer() returns a networkx digraph such that 子 and 宀 are ancestors of 字, and vice versa for descendants.
Then I wrote this script to generate valid puzzles.
from operator import itemgetter
from typing import *
import collections
import decomposer as decomposer_lib
import random
# Get the thirty most common radicals from the graph, weighted by how often
# they appear as subcomponents. (That's why we iterate thru predecessors(n)
# below.)
def most_common_radicals(graph) -> List[Text]:
common = collections.defaultdict(int)
for n in graph.nodes():
for k in list(graph.predecessors(n)):
common[k] += 1
res = dict(sorted(common.items(), key=itemgetter(1), reverse=True)[:30])
return list(res.keys())
# If a character is in the first Unicode CJK plane, it probably has a
# rendering in most web browsers. (This assumption is flawed.)
def has_rendering(i: int) -> bool:
return 0x4E00 <= i <= 0x9FFF
# Given a character, find the set of characters with which it shares a descendant.
# Example: 宀 and 子 are coparents of 字.
def coparents(graph, node): # returns set[node]
cpts = set()
for succ in graph.successors(node):
if not has_rendering(ord(succ)):
continue
preds = list(graph.predecessors(succ))
if len(preds) != 2:
continue
for pred in graph.predecessors(succ):
if not has_rendering(ord(pred)):
continue
if pred != node:
cpts.add(pred)
return cpts
# Given two nodes, returns a list of successors they share.
def children(graph, na, nb): # returns node
s = set.intersection(set(graph.successors(na)), set(graph.successors(nb)))
return list(filter(lambda c: has_rendering(ord(c)), list(s)))
class BoardBuilder:
def __init__(self, graph):
self._graph = graph
# This is the default game described above.
self._cells = [[[1, 5], [1, 6], [1, 7], [1, 8]],
[[2, 6], [2, 7], [2, 8], [2, 9]],
[[3, 0], [3, 7], [3, 8], [3, 9]],
[[4, 0], [4, 5], [4, 6], [4, 9]], ]
# Store our selected categories below.
self._extant = set()
def Build(self):
# Pick four "real categories".
[a, b, c, d] = random.sample(most_common_radicals(self._graph), 4)
# Assign these categories.
[self.assign(n, l) for n, l in zip([1, 2, 3, 4], [a, b, c, d])]
# Assign the red herring categories.
[self.assign(n, self.find_assignment(n)) for n in [5, 6, 7, 8, 9, 0]]
for r_idx, row in enumerate(self._cells):
for c_idx, [a, b] in enumerate(row):
# Pick a random descendant shared by the two components.
self._cells[r_idx][c_idx] = random.sample(
children(self._graph, a, b), 1)[0]
return self._cells
def assign(self, num, ch):
# Replace all instances of |num| with |ch| in self._cells.
for r_idx, row in enumerate(self._cells):
for c_idx, cell in enumerate(row):
for v_idx, v_val in enumerate(cell):
if v_val == num:
self._cells[r_idx][c_idx][v_idx] = ch
self._extant.add(ch)
# Given a category, what other categories share a card with it?
# Example: In the example above, neighbors(1) => [5,6,7,8].
def neighbors(self, num):
others = []
for r_idx, row in enumerate(self._cells):
for c_idx, cell in enumerate(row):
if num not in cell:
continue
others.append(list(filter(lambda n: n != num, cell))[0])
return others
# For our red herring categories, find a CJK character which can sit in for
# |num|, i.e. is a coparent with each of the neighbors.
def find_assignment(self, num):
others = self.neighbors(num)
coparents_list = [coparents(self._graph, o) for o in others]
candidates = set.intersection(*coparents_list)
candidates -= self._extant
return random.sample(list(candidates), 1)[0]
if __name__ == "__main__":
d = decomposer_lib.Decomposer()
for row in BoardBuilder(d._graph).Build():
print(row)
Running this script generates a valid, unshuffled puzzle such as 窠窒岤空洷溄江沚食仚仝企踉踝跮趾.
Making the game⌗
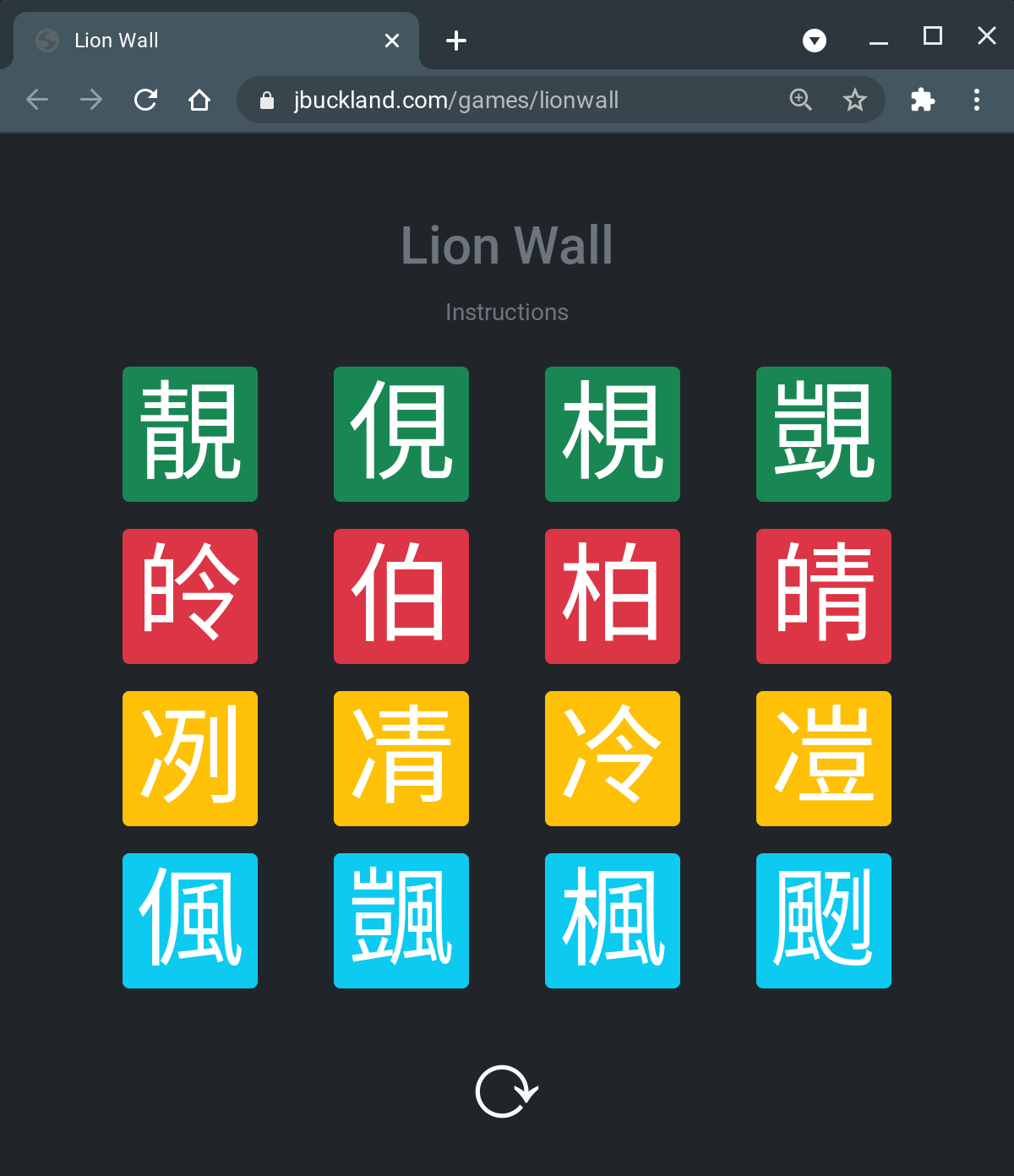
Then I wrote a webpage which could consume these puzzles and display them in an interactive format. You can visit https://jbuckland.com/games/lionwall.html to play the game or you can view the source of the webpage to see how it works.
Semaphores⌗
I wanted cards to animate (flip over, fade out, wait, reappear at the top of the page), but I didn’t want the UI to be interactive during those times. So I wrote a semaphore to ensure that the UI could not be changed while animations or timeouts were ongoing. My solution was a global counter semaphore and two methods:
- a
sleep()timeout which incremented the semaphore, ran the callback, then waited until it was done to decrement the semaphore, and - a
ensureSemaphoreZero()blocker which waited untilsemaphorewas 0 until running.
var semaphore = 0
function ensureSemaphoreZero() {
return new Promise(function (resolve, reject) {
(function waitForSemaphoreZero() {
if (semaphore == 0) return resolve();
setTimeout(waitForSemaphoreZero, 10);
})();
});
}
const sleep = (milliseconds) => {
semaphore++
return new Promise(resolve => {
setTimeout(resolve, milliseconds)
}).then(() => {
semaphore--
})
}
This let me chain sleep callbacks for running spaced-out animations:
sleep(100).then(() => {
// Manipulate the webpage.
sleep(100).then(() => {
// Once that's done, manipulate the webpage again.
})
})
But also react to keystrokes in a blocking way:
function onClickCallback() {
ensureSemaphoreZero().then(() => {
// React to callback.
});
}
Future work⌗
I generated ~100 games for Lion Wall but I ought to go back and generate more. I could also make this game more like the Only Connect version, with a timer, limited guesses, and extra points for specifying the connecting themes.